Números complexos
Para detalhes clique aqui.
Forma retangular:
Forma polar:
Forma trigonométrica:
Forma exponencial:
Forma de Euler:
Exemplo:
Exercício:
Dado o seguinte plano cartesiano que representa um número
complexo. Coloque em todas as formas.
Operações com números
complexos.
Sejam os números
Ẑ1 = a +jb = Z1 ےθ
Ẑ2 = c +jd = Z2ﮮΦ
Adição
Ẑ1 + Ẑ2
= (a + jb) + (c + jd)
Ẑ1 + Ẑ2
= a +jb + c + jd
Ẑ1 + Ẑ2
= (a + c) + j(b + d)
Ẑ1 + Ẑ2
= Ẑ2 + Ẑ1
Subtração
Ẑ1 – Ẑ2
= (a + jb) – (c + jd)
Ẑ1 – Ẑ2
= a + jb – c + jd
Ẑ1 – Ẑ2
= (a – c) + j(b – d)
Ẑ1 + Ẑ2
≠ Ẑ2 + Ẑ1
Multiplicação
Ẑ1 *
Ẑ2 = (a + jb) * (c + jd)
Ẑ1 *
Ẑ2 = ac + ajd + jbc + j²bd
Ẑ1 *
Ẑ2 = ac + ajd + jbc – bd
Ẑ1 * Ẑ2 = (ac – bd) +
j(ad + bc)
Ẑ1 *
Ẑ2 = Ẑ2 * Ẑ1
Divisão
Ẑ1 / Ẑ2
= (a + jb) / (c + jd)
Observação:
conjugado do número complexo (Z*2)
Z*2 = c – jd
Para simplificar a multiplicação e a divisão de números
complexos, nesses casos faremos estas operações com os números na forma polar.
Multiplicação na
forma polar
Divisão na forma
polar
Exemplo:
Ẑ1
= 3 + j4 = 5ے53º
Ẑ2
= 4 + j3 = 5ﮮ37º
Ẑ1
* Ẑ2 = 5ے53º * 5ﮮ37º = 5*5
ﮮ(53º +
37º) = 25ﮮ90º
Ẑ1
/ Ẑ2 = 5ے53º / 5ﮮ37º = (5 / 5)ﮮ(53º - 37º) = 1ﮮ16º
Exercícios-exemplo:
Sem uso de calculadora converter de forma retangular para
polar e de polar para retangular.
1) Ẑ = 10 +
j8
Solução
Ẑ = 10 + j8
(está no 1º quadrante)
│Ẑ│= √(10² + 8²) ≈ 12,8
θ =
arctan(8/10) ≈ 39º
Logo, Ẑ = 12,8ﮮ39º
2) Ẑ = – 5 –
j12
Solução
Ẑ = – 5 –
j12 (está no 3º quadrante)
│Ẑ│= √((-5)² + (-12)²) = 13
Como está no 3º quadrante: θ = [arctan(12/5) ±
180º] ≈ [67 ± 180] = 247º ou – 113º
Logo, Ẑ = 13ﮮ247º ou 13ﮮ -113º
3) Ẑ = – 40 + j50
Solução
Ẑ = – 40 +
j50 (está no segundo quadrante)
│Ẑ│= √((-40)² + 50²) ≈ 64
Como está no 2º
quadrante:
θ =
[arctan(50/(-40) ± 180º] ≈[51º ± 180º] = 129º ou – 231º
Logo, Ẑ = 64ﮮ129º ou 64ﮮ -231º
4) Ẑ = 60 –
j30
Solução
Ẑ = 60 – j30
(está no quarto quadrante)
│Ẑ│= √(60² + (-30)²) ≈ 67
θ =
arctan(-30/(60) ≈ - 27º
Logo, Ẑ = 67ﮮ - 27º
5) 150ﮮ 30º
Solução
Ẑ = │Z│*(cosθ + jsenθ)
(1º quadrante)
Ẑ = 150*(cos30º
+ jsen30º) ≈ 130 + j75
6) 120ﮮ 120º
Solução
Ẑ = │Z│*(cosθ + jsenθ)
(2º quadrante)
Ẑ = 120*(cos120º
+ jsen120º) ≈ – 60 +j104
7) 50ﮮ 220º
Solução
Ẑ = │Z│*(cosθ + jsenθ)
(3º quadrante)
Ẑ = 50*(cos220º
+ jsen220º) ≈ – 38 –
j32
RESISTOR em CA (corrente alternada)
Nas equações acima observamos que:
Fase da tensão = ωt
Fase da corrente = ωt
Diagrama fasorial
Não existe defasagem entre tensão e corrente no resistor.
(tensão e corrente estão em fase).
Notação complexa
R será sempre um número real.
Exemplo: R = 30Ω
CAPACITOR
C: capacitância do capacitor,
Unidade: faraday (F)
Reatância capacitiva (Xc)
– Unidade: Ohms (Ω)
Exemplo – exercício
Calcular a reatância capacitiva para os seguintes dados:
C = 2μF e f
= 60 Hz
Xc = 1/2πfC=
1/ 2π60.2x10-6 =
1326,3 ↔ Xc = 1326,3Ω
CAPACITOR em CA (corrente alternada)
Fase da tensão = ωt
Fase da corrente = (ωt
+ 90º)
Diagrama fasorial
Existe uma defasagem entre tensão e corrente.
A corrente está 90º adiantada em relação à tensão.
Notação complexa
Xc será sempre um
número imaginário negativo.
Exemplo – exercício
INDUTOR
L: indutância do indutor.
Unidade: Henry (H)
Reatância indutiva (XL)
– unidade ohms (Ω)
Exemplo - exercício:
Sabendo-se que f = 60 Hz e L = 0,5 H. Calcular o valor de XL.
XL = 2πf.L
XL = 2*3,14*60*0,5
= 188,4 Ω
INDUTOR em CA
(corrente alternada)
Fase da tensão = ωt
Fase da corrente = (ωt
– 90º)
Diagrama fasorial
Existe uma defasagem entre tensão e corrente.
A corrente está 90º atrasada em relação à tensão.
Notação complexa
XL
será sempre um número imaginário positivo.


















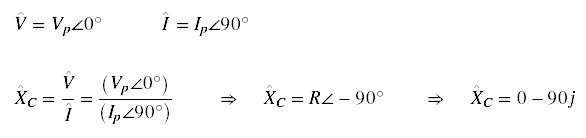






Nenhum comentário:
Postar um comentário