Diodo Zener

Símbolo e polarização

Curva característica

O diodo zener é um tipo de semicondutor que se caracteriza por possuir os lados da Junção mais fortemente dopados, fazendo com que a tensão de ruptura caia para valores bastante baixos.

Observamos na curva característica que para uma variação de corrente entre Iz_k e Iz_Max  a tensão Vz é praticamente constante.

O fabricante fornece os seguintes parâmetros:

Caso não tenhamos a informação do valor de (I_z)_k podemos adotar:

Circuito regulador de tensão:

Nota: Rs = resistor limitador de corrente (deve ser dimensionado para que o Iz não ultrapasse Iz_máx .

Considerando apenas a variação da carga (portanto, R_S, V_E  e V_z constantes):

*Análise:

*Na pior condição possível:

Dimensionamento do R_S (valor e potência):

Calculando (R_L)_min:

Calculando (I_L)_max:

Exercício-Exemplo-1:

Dados o circuito abaixo e os parâmetros a seguir:

(Pz)max = 400 mW

Vz = 6 V

Projetar o circuito.

Exercício-Exemplo-2:

Dados V_e=18 V e V_L= 12V

Z₁ {V_z = 10V, (P_z)_Max = 1,2W}

Z₂ {V_z = 12V, (P_z)_Max = 1,2W}

Escolher o zener e calcular:

1)    (I_z)_Max

2)    (I_z)_k

3)    V_S

4)    R_S

5)    (P)R_S

6)    (I_L)_Max

7)    (R_L)_Min

(I_z)_Max = 1,2/12 = 0,1 A = 100 mA

(I_z)_k = 0,1*(I_z)_Max  = 0,1*100 = 10 mA

Vs = Vê – Vz = 18 – 12 = 6 → VS = 6 V

Rs = Vs/Is = Vs/(I_z)_Max = 6/0,1 = 60 →  Rs = 60 Ω

(I_L)_Max = (I_z)_Max – (Iz)k = 100. 10^-3 – 10.10^-3 = 90 mA

(R_L)_Min = V_L/(I_L)_Max = 12/90.10^-3 = 133,3 Ω

Capacitor em Corrente Contínua

Circuito RC

Um circuito resistor-capacitor (circuito RC), filtro RC ou malha RC, é um dos mais simples filtros eletrônicos de resposta de impulso infinita analógicos.

Figura-01: Circuito RC, para estudo na carga e descarga do capacitor C.

1) Na carga do capacitor C
    (Capacitor em Corrente Contínua)

E = R.i + Vc → E = R.i + q/C, onde q = carga no capacitor
R.i = E – q/C

Portanto, a carga instantânea no capacitor é:

Logo:
Para t = 0 → q = EC (1-1) = 0 → q = 0
Para t = ∞ → q = EC (1-0) = EC → q = EC



A tensão instantânea sobre o capacitor é:

Determinando a corrente na malha:

Usando a lei da conservação de energia, ou considerando as quedas de potenciais no resistor e no capacitor.

Seja q a carga no capacitor e i a corrente no circuito em um dado instante após a chave SW ter sido ligada. As diferenças de potenciais entre os terminais do resistor e do capacitor podem ser escritas por:

Derivando ambos os lados da equação (Eq.03) em relação ao tempo e considerando que E é uma constante, tem-se:

Resolvendo esta equação diferencial ou integrando ambos os membros em relação ao tempo, tem-se:

É a equação que dá a corrente instantânea.

Gráficos

O gráfico-1 ilustra a tensão e a corrente sobre o capacitor em função do tempo.

O gráfico-2 ilustra todos os parâmetros do circuito RC, na carga do capacitor.




Evolução temporal da corrente no circuito RC.

Evolução temporal da carga no capacitor no processo de carregamento.

2) NA DESCARGA DO CAPACITOR

Portanto, a equação da corrente de descarga é:

Logo:
Para t=0 → Imax=(-E/R) é negativo porque a carga está diminuindo.
Para t→∞ → I=0

Diodo como retificador

O diodo tem a característica de conduzir corrente somente num sentido e devido a esta característica unidirecional, o mesmo é utilizado para retificar. O diodo ideal com polarização direta comporta como uma chave fechada e com polarização reversa comporta como uma chave aberta. O diodo real tem resistência direta muito baixa e resistência reversa muito alta.

Os circuitos retificadores convertem uma corrente alternada em corrente contínua.

RETIFICADOR DE MEIA ONDA

Figura 1 – Circuito Retificador de Meia Onda a diodo com carga puramente resistiva.

Descrição do funcionamento:

Para o ponto A (positivo) em relação ao ponto B o diodo está polarizado diretamente e conduz e com isto, a corrente circula de A até B passando pelo diodo e RL.
Para o ponto A (negativo) em relação ao ponto B o diodo está polarizado inversamente e não conduz.
Tem-se corrente em RL, somente, nos semi-ciclos positivos de entrada.
Os semi-ciclos positivos passam para a saída e os semi-ciclos negativos ficam no diodo.

A freqüência de ondulação na saída é igual à freqüência de entrada.

RETIFICADOR DE ONDA COMPLETA

Figura-2: Retificador de onda completa com derivação central (=central tape) com carga resistiva.

Descrição do funcionamento:

Notamos que o ponto médio do enrolamento secundário do transformador está ligado à terra. Por isso, realiza um retificador de ponto médio, equivalente a dois retificadores de meia-onda, cada um com uma tensão de entrada igual à metade da tensão secundária. O diodo D1 conduz durante as alternâncias positivas e o diodo D2 durante as alternâncias negativas. Daí resulta que a corrente retificada na carga passa nas duas alternâncias. O retificador de ponto médio comporta-se como dois retificadores de meia-onda refletidos entre si.

A freqüência de ondulação na saída é o dobro da freqüência de entrada.

Figura-3: Retificador de onda completa com ponte de diodos com carga resistiva.

Descrição do funcionamento:

O retificador em ponte dispensa o uso do transformador com tomada central e com isto, pode-se ter um retificador de onda completa ligado diretamente à rede elétrica. Quando A é positivo em relação a B, a corrente sai de A passa por D1, RL, D3 e chega ao ponto B (Figura-4). Quando A é negativo em relação a B, a corrente sai de B passa por D2, RL, D4 e chega ao ponto A (Figura-5). Conduzem somente dois diodos de cada vez. Quando o ponto A é positivo D1 e D3 conduzem. Quando o ponto A é negativo D2 e D4 conduzem. Para qualquer polaridade de A ou de B a corrente IL circula num único sentido em RL e por isto, a corrente em RL é contínua. Somente os semiciclos positivos passam para a saída.

A freqüência de ondulação na saída é o dobro da freqüência de entrada.

Figura-4:  Nos semiciclos positivos (em vermelho o caminho da corrente)

Figura-5:  Nos semiciclos negativos (em vermelho o caminho da corrente)


Retificador de Meia Onda com Filtro Capacitivo

A colocação de um capacitor em paralelo (que funciona como filtro) com a carga melhora o desempenho do circuito através da diminuição do ripple (=flutuação da tensão ao redor de um valor médio) e do aumento na tensão contínua (para um mesmo valor de tensão alternada).

Figura-06: Retificador de meia onda com filtro capacitivo

Figura-07: Formas de onda de entrada (azul) e saída [sobre a carga] (vermelho)

Na filtragem, normalmente, é utilizado um capacitor eletrolítico de grande valor ligado à saída DC para agir como um reservatório, fornecendo corrente para a saída quando a tensão DC varia no retificador. A figura-07 mostra a tensão de entrada AC e a de saída DC suavizada.

Após o pico, o capacitor descarrega-se através da resistência (=carga), até o momento em que a tensão retificada exceda a tensão do capacitor. O capacitor é, novamente, carregado e o processo se repete.

A filtragem seria melhor (=até perfeita) se a tensão do capacitor ficasse estável (=fixo) durante as descargas, resultando em ripple muito menor (ou até desprezível). Porém, durante as descargas existe uma queda de tensão do capacitor, que resulta em ondulações de tensão (tensão de ripple) não desprezível.

Podemos calcular (=estimar) o valor (aproximado) do ripple através da seguinte fórmula empírica:

Retificador de Onda Completa com Filtro Capacitivo

A filtragem para o retificador de onda completa é mais eficiente do que para o retificador de meia onda. Em onda completa o capacitor será recarregado 120 vezes por segundo. O capacitor descarrega durante um tempo menor e com isto a sua tensão permanece próxima de Vp até que seja novamente recarregado. Quando a carga RL solicita uma alta corrente é necessário que o retificador seja de onda completa.

Figura-08: Retificador de onda completa com filtro capacitivo

Figura-09: Forma de onda da tensão Vo

Podemos calcular (=estimar) o valor (aproximado) do ripple através da seguinte fórmula empírica:

Curva do diodo e reta de carga – Exercícios Resolvidos

1)     EX-01

Conhecidos os seguintes dados:

1)     PR = 90 mW

2)     PD = 30 mW

3)     IDQ = 15 mA

Calcular:

a)     VR e RL

b)     VDQ e RD

c)      IDmax e E

d)     Pf

Resolução:

1) Vamos calcular os valores de VR e RL (na carga)
Foram dados: PR = 90 mW e IDQ = 15 mA

Sabemos que a potência na carga é igual à resistência multiplicada ao quadrado da corrente que atravessa esta. Logo, temos que:

PR = RL*I²DQ   ↔  90mW = RL* (15mA)²   ↔  RL = 400 Ω

Lei de Ohm: a tensão na carga é igual ao produto da resistência pela corrente que atravessa esta. Logo, temos que:

VR = RL*IDQ  ↔  VR = 400*(15mA)  ↔  VR = 6 V

2) Vamos calcular os valores de VDQ e RD (no diodo)

Foram dados: PD = 30mW e IDQ = 15 mA

Idem ao anterior: a potência no diodo é igual à resistência interna do diodo multiplicada ao quadrado da corrente que atravessa esta. Logo, temos que:

PR = RL*I²DQ   ↔  30mW = RD* (15mA)²   ↔  RD = 133,33 Ω

Pela lei de Ohm, temos que:

VD = RD*IDQ  ↔  VD = 133,33*(15mA)  ↔  VDQ = 2 V

3) Vamos calcular os valores de IDmax, E (na bateria)

O valor de E é a soma de VR e VDQ , logo temos que:

E = VR + VDQ  ↔  E = 6 + 2 = 8  ↔  E = 8 V

Para calcular o IDmax devemos considerar que o diodo está em curto (=diodo ideal, resistência interna zero).

IDmax = E/RL   ↔  IDmax = 8/400 = 0,020  ↔ IDmax = 20 mA

4) Vamos calcular o valor de Pf

A potência da bateria é a soma das potências no diodo e na carga (conservação de energia), logo temos que:

PD = 30mW e PR = 90mW  foram dados:

 

Pf  = PD + PR   ↔   Pf  = 30 + 90 = 120  ↔  Pf  = 120mW

2)     EX-02

Dado a curva característica de um diodo e a reta de carga na polarização direta de um diodo, determinar:

1)     E, VDQ, IDQ, Imax

2)     RD

3)     VR, RL

4)     PD, PR, Pf

Resolução:

Calcular E, VDQ, IDQ e Imax

Pela observação e interpretação da figura dada:

Quando a corrente ID=0, então temos VD = 12 = E  → E = 12V

O ponto de operação (ou ponto quiescente) possui coordenadas (VDQ, IDQ), logo:  VDQ = 5V e IDQ = 14mA

O valor da corrente no ponto onde a reta de carga intercepta o eixo da corrente ID corresponde à corrente máxima.

Logo, pela figura: Imax = 24mA

Calcular a RD:

Aplicando a Lei de Ohm: 

VDQ = RD*IDQ  ↔  RD = VDQ/IDQ = 5/14mA = 357,14 Ω ↔ RD=357,14Ω

Calcular a RL e VR:

IDmax = E/R  ↔  RL = E/IDmax  = 12/24mA = 500 Ω ↔  RL = 500Ω

Aplicando a Lei de Ohm:

VR = RL*IDQ = 500*14mA = 7 ↔  VR = 7V

Ou:  E = VDQ + VR  ↔  VR = E – VDQ  = 12 – 5 = 7 ↔  VR = 7V

Calcular:  PD, PR e Pf

PD = RD * I²DQ = 357,14*(14mA)²  ≈ 70mW  ↔  PD = 70 mW

PR = RL * I²DQ = 500*(14mA)² = 98mW  ↔  PR = 98 mW

Pf = PD + PR = 70 + 98 = 168mW  ↔  Pf = 168 mW

3)     EX-03

O circuito abaixo apresenta um problema.

Identifique-o, propondo uma solução

Solução:

a)     Vamos calcular a corrente I do circuito dado.

A tensão da bateria é a soma das tensões no diodo e resistor. Logo temos que:

10 = 0,7 + 5*I  ↔  I = (10 – 0,7)/5 = 1,86 A

b)     Agora vamos calcular a potência dissipada no diodo do circuito dado:

Vɣ = 0,7V (tensão de joelho que foi dado)

PD = VD*I =  0,7*1,86 = 1,3 W

Conclui-se que o resistor está sub-dimensionado.  Pois, os valores de ID e PD calculados são maiores que os valores que foram dados.

Vamos calcular o valor mínimo da resistência (Rmin) necessária para que o diodo funcione corretamente dentro das características informadas:

Temos as seguintes informações:

a) ID = 0,8A

b) Vɣ = 0,7V

Portanto,

10 = 0,7 + Rmin*0,8  ↔  Rmin=(10 – 0,7)/0,8 = 11,6Ω  → Rmin = 11,6Ω

Logo, poderíamos aplicar uma resistência de 12Ω (=valor comercial)

O valor da potência do resistor:  P = R* I² = 12*0,8² = 7,68 W, logo devemos utilizar uma resistência de 12Ω de 10W 

4)     EX-04

Verifique as condições (1,2, ou3) das lâmpadas do circuito abaixo:

Condições:

1)     As lâmpadas que acendem;

2)     As lâmpadas que não acendem;

3)     As lâmpadas que acendem com sobrecarga e podem queimar.

Solução:

Fazendo uma análise visual, temos que L1 e L3 não acendem porque o diodo está reversamente polarizado.

Refazendo a figura, eliminando L1 e L3:

Observando a nova figura e considerando que todos os diodos são iguais e todas as lâmpadas também iguais.

I1 = 2*I2

Vamos analisar a lâmpada L2:

Supondo que o diodo sejam todos iguais de silício (Vɣ = 0,7 V).

E foram dados que: VL = 6V e PL = 120mW

A tensão sobre L2 é igual a tensão da bateria subtraído de Vɣ = 0,7 V; logo temos que:

12 = 0,7 + VL2    →  VL2 = 11,3V

Sendo que a tensão nominal da lâmpada é de 6V.

A lâmpada L2 queimará, porque temos uma condição de sobrecarga.

Supondo que L2 queima, então temos apenas L4 e L5 que acendem.  Vamos verificar estas condições:

12 = Vɣ + 2*VL  ↔  12 = 0,7 + 2*VL  →  VL = (12 - 0,7)/2 = 5,65 V

Calculando a resistência de cada lâmpada (L4, L5):

Foram dados que: VL = 6V e PL = 120mW

Sabemos que:

VL = RL * IL (lei de Ohm)   →  IL = VL/RL

PL = VL * IL = RL * I²L = V²L/RL

Logo:  PL = V²L/RL ↔  RL = V²L/PL = 6²/0,120 = 300Ω   →  RL = 300Ω

Portanto: a corrente no circuito é VL = RL*IL  →  IL = 5,65/300 = 18,8 mA

Então a potência dissipada em cada lâmpada é:  PL = RL*I²L = 300* 0,0188² = 106 mW  (é inferior a 120 mW, portanto, não queima).

Resumo:

1)     As lâmpadas que acendem: L4 e L5

2)     As lâmpadas que não acendem: L1 e L3

3)     A lâmpada que acende com sobrecarga e queima: L2

5)     EX-05

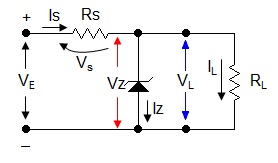
Sabendo-se que Ve = 10 V, VD = 0,7 V e RS = 1 kΩ, determine o valor da corrente do diodo (ID).

Solução:
ID = (Ve – VD)/RS → ID = (10 – 0,7)/1000 = 9,3 mA → ID = 9,3mA

6)     EX-06

Sabendo-se que Ve = 8 V, VD = 0,7 V e RS = 15 kΩ, determine o valor da corrente do diodo (ID).

Solução:
ID = (Ve – VD)/Rs = (8 – 0,7)/15000 = 0,5 mA  →  ID = 0,5mA

O diodo não consegue romper a barreira, porque o valor da Rs é muito grande.

7)     EX-07

Sabendo-se que Ve = 20 V, VD = 0,7 V e RS = 470 Ω, determine o valor da corrente do diodo (ID). 

Solução:

ID = (Ve – VD)/Rs = (20 – 0,7)/470 = 41 mA  →  ID = 41 mA

8)     EX-08

Determine VD, ID e Vo para o circuito da figura a seguir.

Solução:
Vamos supor que o diodo esteja no ponto de operação (quiescente), logo podemos considerar que o VD = 0,7 V aproximadamente.

Portanto,
ID = (100 – 0,7)/(1200 + 4700) = 16,8 mA
Então: VD = 0,7V e ID = 16,8 mA

Calculando o valor de Vo:
Vo = ID*4700 + VD = 0,0168*4700 + 0,7 = 79,7 V → Vo = 79,7 V

9)     EX-09

Determine o valor de Vo do circuito abaixo.

Solução:
Calculando a corrente I, considerando VD = 0,7 V e aplicando a lei de Ohm:

I = (10 – 0,7 – (-2)) / (1200 + 47) = 9 mA

Logo,
Vo – (-2) = 47 * 0,009 → Vo = 0,423 ─ 2 = ─ 1,6 V   →  Vo = ─ 1,6 V

10)     EX-10

Determine Vo e ID para o circuito a seguir.

Solução:
Considerando VD = 0,7 V

Vo – (-5) = VD  →  Vo +5 = 0,7 → Vo = 0,7 – 5 = - 4,3  → Vo = ─ 4,3 V

Portanto, temos que:
20 – Vo = 680*ID  →  20 – (-4,3) = 680*ID →  ID = 24,3/680 =  36 mA
→  ID = 36mA